Blog
Vizualizacija visokodimenzionalnih podataka
U svijetu strojnog učenja nerijetko se barata sa skupovima podataka čije su dimenzije (broj značajki) reda veličine nekoliko tisuća. Također, budući da mi kao ljudi nismo sposobni percipirati dalje od treće dimenzije, takvi podatci nam uvelike otežavaju nalaženje ikakvih smislenih uzoraka unutar njih i to je zapravo tema ovog blog posta, metode kojima možemo uzeti visokodimenzionalne podatke koje je nemoguće vizualizirati i nekako ih spustiti u 2D ili 3D prostor i vizualizirati ih jer, kako poznata izreka govori, slika govori 1000 riječi. Metoda ima mnogo, ali ovdje ćemo se dotaknuti tek tri koje se ubrajaju među najpoznatije: PCA, t-SNE i UMAP. Također će svaka od metoda biti isprobana na standardnom MNIST skupu podataka ručno pisanih znamenki kako bismo mogli i vidjeti koliko uspješno pojedina metoda obavlja svoj zadatak.
PCA (Principal Component Analysis)
PCA je možda najpoznatija metoda za reduciranje dimenzija podataka. Pri reduciranju dimenzija, naravno, neminovan je gubitak određene količine informacije. Upravo zato je i glavna ideja iza ovog postupka da se pronađe potprostor zadanih nižih dimenzija koji najbolje prikazuje pojedini razred uzoraka na način da pogreška između originalnog uzorka i projekcije uzorka u taj potprostor bude minimalna, odnosno da bude sačuvana maksimalna varijacija u podatcima. U ovom blogu neću ulaziti u detalje kako PCA, ili bilo koja druga spomenuta metoda funkcionira, ali valjalo bi spomenuti neke od glavnih točaka.
Glavna ideja temelji se na konstrukciji svojstvenih komponenti (naslovne Principal Components) odnosno linearnih kombinacija inicijalnih varijabli. Geometrijski rečeno, svojstvene komponente predstavljaju pravce koji objašnjavaju maksimalnu količinu varijacije, odnosno pravci koji nose najviše informacija. Budući da postoji jednako svojstvenih komponenti koliko ima i dimenzija u podatcima, one se konstruiraju tako da uvijek prva svojstvena komponenta sadrži najveću moguću varijaciju u skupu podataka. Sljedeća svojstvena komponenta se računa na isti način uz uvjete da je ortogonalna na prošlu i sadržava opet maksimalnu varijaciju (doduše nužno manju od prošle).
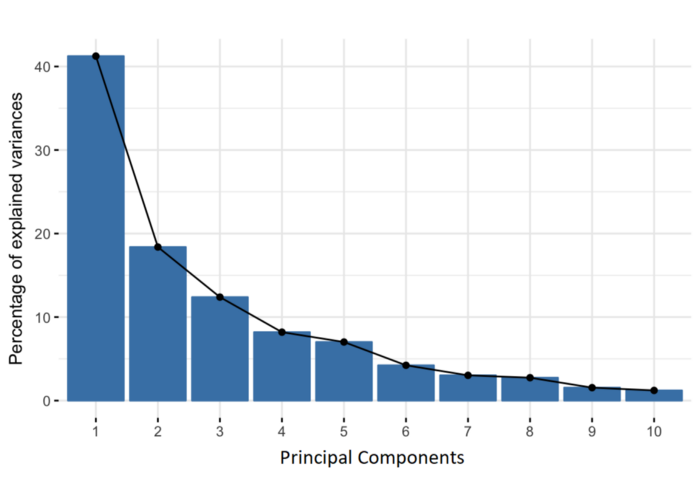
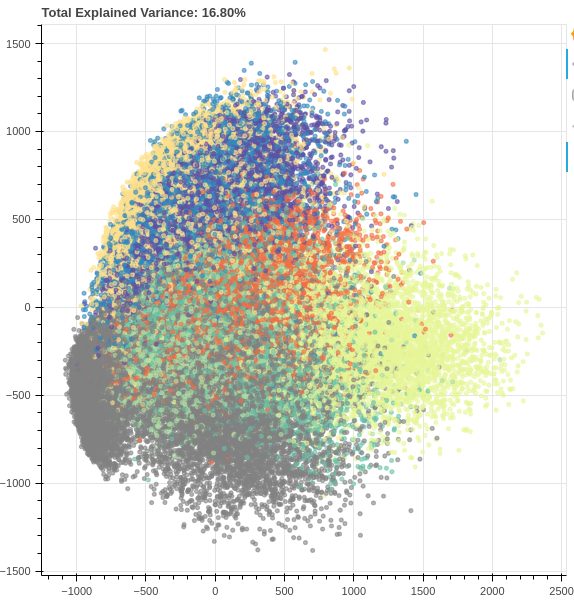
Na gornjoj slici vidimo primjenu PCA na MNIST skupu podataka ručno pisanih znamenki (784 na 2 dimenzije). Iako vidimo neko odvajanje među primjerima, sa samo dvije komponente zadržavamo samo ~16% varijacije što uistinu nije dovoljno za nekakve spektakularne rezultate. No iako PCA u ovom primjeru za konkretnu svrhu vizualizacije ne daje zadovoljavajuće rezultate, valja napomenuti da već nakon stavljanja broja komponenti na 331, postotak varijacije je ~99% što znači da smo uspjeli smanjiti broj dimenzija za više od pola uz gotovo nepostojeći gubitak informacija. Ovo nam govori da iako PCA možda nije uvijek najpogodniji za problem vizualizacije, itekako može biti od pomoći pri rješavanju nekih drugih problema, kao što je npr. famozni problem tzv. “prokletstva dimenzionalnosti” (kako raste broj značajki, količina podataka koja nam je potrebna da bi model strojnog učenja dao dobre rezultate raste eksponencijalno).
t-SNE (t-distributed Stochastic Neighbor Embedding)
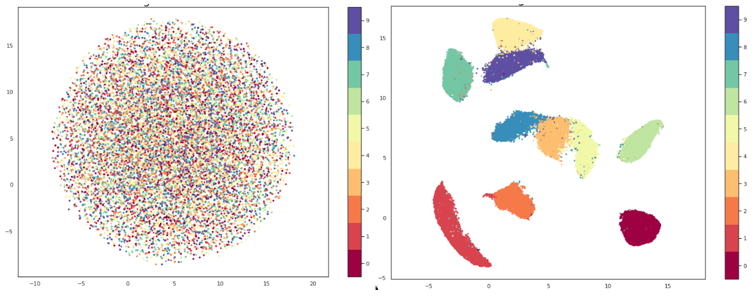
t-SNE je nenadzirana, nelinearna tehnika za vizualizaciju visokodimenzionalnih podataka. Za razliku od PCA-a, koji se pored vizualizacije može koristiti za redukciju dimenzionalnosti u druge svrhe, t-SNE-u je glavna svrha upravo vizualizacija. Za detalje kako t-SNE funkcionira, najbolja je referenca originalni rad, ali vrlo pojednostavljeno rečeno, stvara se distribucija vjerojatnosti u visokodimenzionalnom prostoru (to znači da ako odaberemo točku u skupu podataka, definiramo vjerojatnost da joj je druga točka koju odaberemo susjed). Zatim se kreira niskodimenzionalni prostor koji ima istu (ili koliko je moguće sličnu) distribuciju vjerojatnosti.
Za razliku od PCA, t-SNE minimizira udaljenost između sličnih točaka i ignorira udaljene (tzv. “local embedding”). Ono što je također različito je da t-SNE ima hiperparametre kojima možemo značajno utjecati na krajnji rezultat. Najbitniji je perplexity, varijabla pomoću koje zadajemo algoritmu očekivani broj bliskih susjeda koje bi svaka točka trebala imati. Tipične vrijednosti za perplexity su između 5 i 50. Također je bitno napomenuti da je t-SNE veoma spor i kako bi se mogao koristiti u razumnom vremenu, često je potrebno prvo pretprocesuirati podatke korištenjem PCA-a ili nečega sličnog kako bi se smanjile dimenzije.
UMAP (Uniform Manifold Approximation and Projection)
Slično kao i t-SNE, UMAP je nelinearna metoda za redukciju dimenzionalnosti. Veoma je efektivan u vizualizaciju grupacija i njihovih relativnih blizina i, za razliku od t-SNE-a, ne pati od problema sa sporim izvođenjem tako da pretprocesuiranje nije potrebno. Također kao i sa t-SNE-om neću ulaziti u matematičku pozadinu algoritma, ali čitatelj ju može proučiti u originalnom radu.
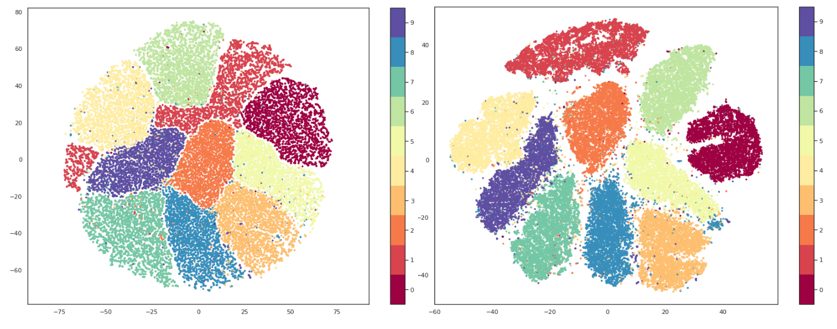
Po samom načinu rada, UMAP i t-SNE su veoma slični, a glavna razlika je interpretacija udaljenosti između grupacija. Kod t-SNE-a očuvane su samo lokalne strukture u podatcima dok UMAP čuva i lokalne i globalne. To znači da s t-SNE-om ne možemo interpretirati udaljenosti između grupa, dok sa UMAP-om možemo, odnosno da ako promatramo tri grupe na grafu napravljenom pomoću t-SNE-a, ne možemo donositi pretpostavke o tome jesu li dvije od tih grupa sličnije samo bazirano na njihovoj udaljenosti na grafu, dok bi korištenjem UMAP-a to trebali moći.
Upravo se zbog toga, kao i zbog veće brzine, UMAP generalno smatra kao efektivnije rješenje za vizualizaciju u odnosu na t-SNE. UMAP također ima parametar n_neighbors koji služi približno sličnoj svrsi kao perplexity za t-SNE. Tim parametrom se odlučuje koliki će biti broj najbližih susjeda koji će se koristiti u izradi inicijalnog visokodimenzionalnog grafa, odnosno kontrolira se kako će UMAP balansirati lokalne i globalne strukture. S nižim vrijednostima fokusirat će se više na lokalne strukture, ograničavajući broj susjednih točaka koje će se razmatrati pri analizi podataka, dok će se s višim vrijednostima fokus premjestiti na “big-picture” strukture gubeći pritom nešto na suptilnijim detaljima.
Zaključak
Iz svega dosad navedenog bilo bi lako pretpostaviti da je UMAP najbolji, slijedi ga t-SNE, a zatim PCA, no stvari nikada nisu toliko jednostavne. PCA je za ovu svrhu u svakom slučaju lošije obavio posao od ostale dvije metode, ali vizualizacija nije jedina njegova svrha, između ostalog PCA može biti moćan alat u borbi protiv ranije spomenutog “prokletstva dimenzionalnosti”, no čini se da UMAP ipak daje bolji balans između lokalnih i globalnih struktura te nam, zahvaljujući inovativnim rješenjima u kreaciji približnih procjena visokodimenzionalnih grafova umjesto mjerenja svake pojedine točke, uvelike može uštedjeti na vremenu. Međutim, uvijek treba držati na umu da je svaki problem jedinstven i ne postoji “magični metak” za sve te se uvijek u pronalasku rješenja problemima treba pristupati individualno.
Reference:

