Blog ENG
Image Augmentation with TensorFlow
Image augmentation is a procedure, used in image classification problems, in which the image dataset is artificially expanded by applying various transformations to those images. The purpose of image augmentation is two-fold. Firstly, model accuracy and precision are increased by closing the gap between train and test data. Secondly, model generalizability is increased by forcing our model to really learn semantic differences between classes and not to memorize specific parameters and the theme of the dataset.
We shall now list some of the possible augmentations:
- rotation,
- translation,
- sheering,
- reflection,
- contrast adjustment,
- brightness adjustment,
- sharpness adjustment,
- hue adjustment,
- saturation adjustment,
- random cutout.
The first four augmentations from the list are called affine augmentations, while the next five are called pixel-wise augmentations. Image 1 shows a particular affine augmentation, rotation, while image 2 shows various pixel-wise augmentations.


saturation in bottom-left, hue in bottom-righ
Determinism
Of course, we want augmentations to be performed randomly both probability-wise and magnitude-wise. That way we can prevent our model from memorizing the specific style, thus forcing it to really learn what separates classes. However, not all randomnesses are made equal, we expect our program to yield reproducible results over repeated runs. The secret lies in the fact that random numbers generated by programming languages are not random in the true sense of the word. They are obtained by feeding a seed to a nonlinear, complicated function. Such a function will always return the same result, provided that the seed is the same, but if we were to perturb the seed slightly, we would generally get a vastly different result. Therefore, our random number generator has a very high entropy, thus it appears to be random. Random numbers generated in such fashion are called pseudorandom.
Images as tensors
At first glance, an image appears to have two dimensions, width and height. But color cannot be parametrized by a single number, so alongside the 2 spatial dimensions we are required to add an additional, color dimension. Moreover, during the deep model training, the dataset is usually divided into batches of a particular size. Each batch can be thought of as a function which maps ordered four values (N, W, H, C) to the pixel value, where N stands for batch index, W and H for column and row index respectively and C for color channel. Such an object is known as the rank-4 tensor and a firm grasp of its algebra is required to be competent in computer vision. A very nice tool in our toolbox is the function tf.einsum(). It is based on the Einstein’s summation convention. Let’s consider a basic matrix multiplication: (as we know, matrices are nothing but rank-2 tensors)
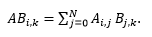
In the Einstein’s summation convention the sum symbol is omitted as the summation is implied over all indices that appear twice (fun fact: Einstein called this convention his “greatest contribution”). Thus, the equation above can be written as:
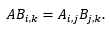
Using tf.einsum() it would become:
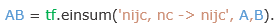
In the following chapter, we shall delve a little bit deeper into TensorFlow, and use the knowledge acquired so far to make a small image augmentation pipeline.
Example
In this example we will use the TensorFlow package in the Python programming language. TensorFlow is a powerful package which enables us to work with graphical models where edges are tensors and vertices are operations. Hence, the name tensor-flow is appropriate.

Let’s now define the function which takes a batch of images and applies a contrast adjustment to each image separately. Such a function would take 2 arguments, a rank-4 tensor – batch of images (images) and a rank-1 tensor – magnitudes of contrast adjustments for each image (factors). Note that the first dimension of both tensors should be equal. Let x be the change factor, and m the mean values of pixel intensity of image with batch index n and channel index c. Then the image pixels adopt the following value:
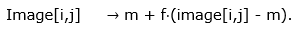
As we can see from the expression, when f = 1, no contrast adjustment takes place. On the other hand, when f = 0, all pixels are set to the mean value.

Now we need a function which generates random numbers that will be used to determine magnitudes and probabilities for augmentations. This function will then call dedicated augmentation functions, as the one above, and return an augmented batch of images. Its arguments are a batch of images, labels and a seed. Note that the function tf.random.stateless_uniform() is used rather than tf.random_uniform(). The reason lies in the fact that the former is independent of the global seed and is deterministic with respect to the seed, which doesn’t hold for the latter.

In the end we have to make a data-loading function, which batches our dataset and sends it through our augmentation pipeline. During the process, such a function has to generate a deterministic sequence of random numbers which will be utilized to determine the probabilities and magnitudes of the augmentations.
Let’s assume that the dataset is in the tf.data.Dataset format. Such a dataset is then, alongside the specified batch size fed to the function generate_batches(). Its arguments are dataset (data), batch size (batch_size) and boolean which determines whether augmentations will be applied or not (train). The function f(batch_seed, D) mediates between the tf.data.Dataset module and our augmentations pipeline.


Conclusion
In this blog we got familiar with the basic concepts of image augmentation. We also discussed problems of determinism and reproducibility and demonstrated a way in which those problems can be resolved using TensorFlow. Finally, we constructed a simple augmentation pipeline that is deterministic, reproducible and applies transformations to each image separately, which is not true if we were to use premade augmentations available in TensorFlow. Image augmentation is useful because it enables us to make more precise and robust models when we don’t have an access to large volumes of diverse data.

