Blog ENG
News and trends in the world of data science

In the previous blog post about news in the world of data science, we wrote about data sonification and the latest achievements in that area. This time we will write about DeepMind’s new paper, the algorithm it introduced, and what it means for computer science and the world of artificial intelligence. Early last month, DeepMind published a paper in Nature presenting AlphaTensor, the first artificial intelligence system to discover new and efficient algorithms for performing some fundamental mathematical operations, such as matrix multiplication.
Matrix multiplication
Matrix multiplication is one of the most important and common mathematical operations used in modern computing. This operation is in the background of numerous optimization algorithms, as well as numerical algorithms of linear algebra.
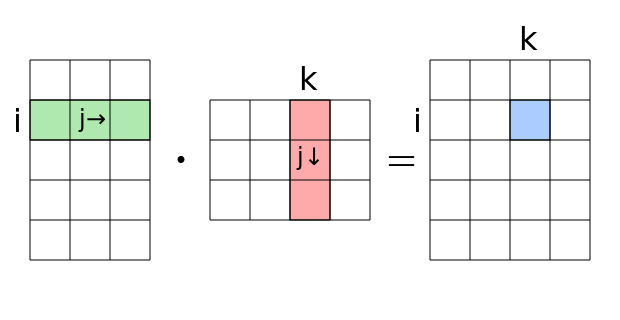
Matrix multiplication is one of the most fundamental and computationally intensive operations in machine and deep learning. Since neural networks can be expressed by matrices, the matrix multiplication operation is one of the most important operations when it comes to deep neural networks. Today, large datasets are also expressed using matrices. For example, in the bag of words model, each row of the matrix corresponds to one document. Images are also expressed as three-dimensional matrices, where one pixel of the image is expressed by a 3D vector as an element of the matrix. Since matrices represent so much of the data we own and use, it’s no surprise that companies around the world are spending large amounts of resources on developing computer hardware to multiply matrices quickly and efficiently. Even the smallest improvements in speeding up this process can significantly reduce the training time of many models used in machine and deep learning.
Mathematicians have used the same method of matrix multiplication for centuries, which is still familiar to us today. However, in 1969, the German mathematician Volker Strassen presented a more efficient way of multiplying matrices, which, when multiplying two 2×2 matrices in addition to multiple addition operations, used seven multiplication operations, as opposed to the previous eight.
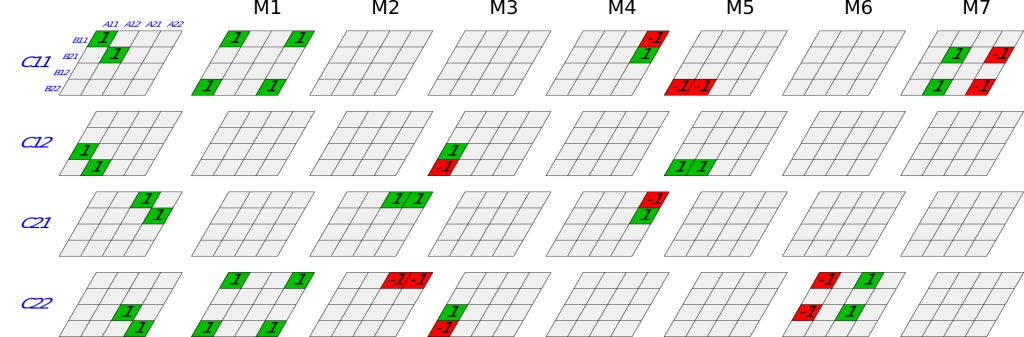
AlphaTensor
In the paper published in Nature, DeepMind investigated how modern artificial intelligence techniques can advance the discovery of new matrix multiplication algorithms. AlphaTensor has discovered algorithms that are more efficient than some state-of-the-art techniques for multiplying matrices of various sizes, and these algorithms outperform those designed by humans, which is a major advance in the field of algorithmic discovery. AlphaTensor is built on lessons learned from its predecessor AlphaZero, an already well-known agent that has shown superhuman performance in board games such as chess and Go. This shows that AlphaZero is a very powerful algorithm that can be extended far beyond its domain to help solve current mathematical problems.

The problem of finding efficient algorithms for matrix multiplication was first turned into a single-player game. In that game, the board is a three-dimensional tensor, showing how far the current algorithm is from being correct. The algorithm gives instructions to the player and the player tries to modify the tensor while staying within the set of allowed moves. When the player succeeds in canceling out the tensor, it means that he has reached the end of the game and that a new matrix multiplication algorithm has been found that is proven to be correct. The efficiency of such an algorithm is measured by the number of steps the player had to take to cancel out the tensor and reach the end of the game.
DeepMind’s approach uses a form of machine learning called reinforcement learning, in which an AI agent, often represented by a neural network, learns to communicate with its environment in order to achieve a goal, which in this case is victory in the game.
The DeepMind team highlighted the difficulty of the seemingly simple problem of multiplying two matrices by comparing the number of possible algorithms the game needs to consider to a much larger number than the number of all the atoms in the universe. The number of possible moves in each step of this game is 30 orders of magnitude greater than the number of possible moves in the game Go, which has been a great challenge for AI for years.
Algorithm performance
Looking at performance, AlphaTensor was able to find an algorithm for multiplying a 4×5 matrix by a 5×5 matrix with an efficiency of 76 multiplications, beating the previous algorithm that required 80 multiplication operations. For a set of larger matrices, 11×12 and 12×12, AlphaTensor was able to reduce the number of multiplications required from 1022 to 990.
These results are an introduction to future research in the field of complexity theory, which deals with determining the fastest algorithms for solving numerous computational problems. Understanding the space of possible algorithms can lead to new insights and results in determining the asymptotic complexity of matrix multiplication, one of the fundamental open problems in computer science. Since matrix multiplication is a key component in many computing tasks, the algorithms discovered by AlphaTensor could soon make computing significantly more efficient.
References:

