Blog ENG
Optimal decision making
We make decisions every day, both in private and in business life. Most of these decisions are made intuitively without much thinking. Sometimes this is because we have found ourselves in a similar situation several times before, so we already “know” what to do. Sometimes we don’t have enough information, so intuition is all we have left. Sometimes, even when we have enough information, the problem seems trivial, and we decide on “common sense” by intuition. However, even when the problem seems trivial, intuition can often deceive us and lead us to make a decision that is not optimal.
Why we need optimization
Let us look at a simple problem of children traveling in a school bus: 300 kids need to travel to the zoo. The school may rent 40 seats and 30 seats buses. The rental price of a 40-seat bus is 500 euros, and a 30-seat bus costs 400 euros. How many buses of each size do you use to minimize cost? Although there may be several options, given the number of buses rented, there is only one solution that minimizes rental costs. At first glance, an intuitive solution would be to fill the big buses first and place the remaining children in a smaller bus (7 large buses and 1 smaller one, which costs 3,900 euros). In this case, there is a better solution where the amount of rent is 3,800 euros. This is possible in case six buses with 40 seats and two buses with 30 seats are rented.

Even such a simple problem shows the need to apply a more reliable way of decision-making that will always give the optimal result. This is even more important in real business problems that have hundreds and sometimes thousands and millions of variables on which to make decisions. Besides that, with real business problems by applying optimization, the return on investment will not be 100 euros as in our problem with the bus, but that amount is calculated in millions.
Optimization is the process of finding the optimal solution from a set of all possible solutions. This set includes all solutions that meet the given conditions and limitations that are set in advance depending on the requirements of the model, and this best solution would be the one that is about minimizing costs (production, transport…) while maximizing profits.
Optimization tools
Although it is possible to do the optimization using MS Excel Solver or some of the open-source tools, I recommend that more complex optimization problems that involve a large number of variables use commercial solutions such as IBM ILOG CPLEX. It is IBM’s award-winning optimization software for solving various types of optimization problems. IBM CPLEX comes from the word “simplex” which means a mathematical algorithm in the field of linear programming. The algorithm is reduced to searching the vertices of the domain of possibility, ie feasibility (vertices of simplex), in order to find in which of these vertices the optimal value of the goal function appears. Within the program itself, it is possible to choose a large number of interfaces and programming languages, and it is possible to create powerful visualizations.
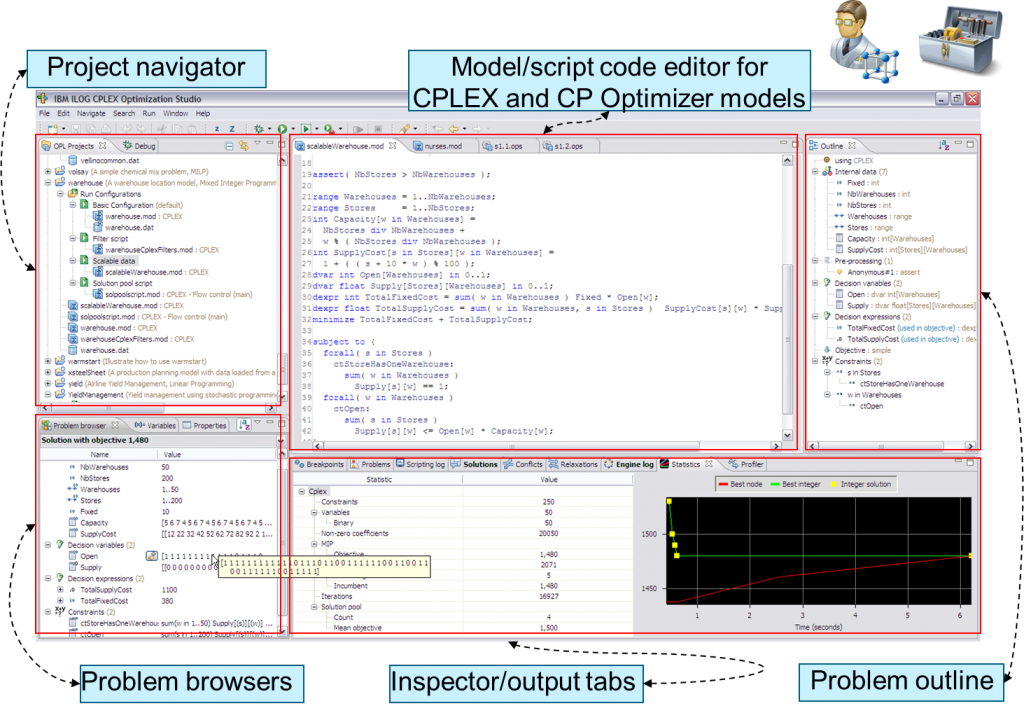
CPLEX uses the OPL programming language. OPL is intuitive and makes it easier to understand the constraints, goals, and costs. For example, the previously mentioned problem with bus rental can be described in the OPL programming language as follows:
int nbKids=300;
float costBus40=500;
float costBus30=400;
dvar int+ nbBus40;
dvar int+ nbBus30;
minimize
costBus40*nbBus40 + nbBus30*costBus30;
subject to
{
40*nbBus40+
nbBus30*30
>=nbKids;
}Optimization models can also be developed in the Java, Python, .NET, C, and C ++ programming languages. For example, the same problem written in Python using the DoCplex library would look like this:
from docplex.mp.model import Model
mdl = Model(name='buses’)
nbbus40 = mdl.integer_var(name='nbBus40')
nbbus30 = mdl.integer_var(name='nbBus30’)
mdl.add_constraint(nbbus40*40 + nbbus30*30 >= 300, 'kids’)
mdl.minimize(nbbus40*500 + nbbus30*400)
mdl.solve()
print(nbbus40.solution_value);
print(nbbus30.solution_value);Conclusion
This was just an example of how optimization can be used to solve a simple problem. In real life, the application of optimization is really wide and there is almost no area of the industry that does not strive to optimize certain business processes. The most common goal is to minimize costs (production, transport…) while maximizing profits and all this while respecting the given limits. In addition to visible savings and higher profits, it also increases the satisfaction of end-users who will receive the goods or services on time.
Reference:

