Warehouse/route/process optimization

Optimization is already a well-known term and optimization models have been an integral part of every serious business for some time. In the USA, optimization methods were developed during World War II primarily for military logistics problems, such as optimizing the transport of troops and equipment in convoys. Optimization, in the simplest terms, is finding the ‘best’ solution from a set of all existing solutions. This set includes all those solutions that meet certain conditions and restrictions that are predetermined depending on the model’s requirements. The best solution would be the one that achieves the highest or lowest value with all the given restrictions.

The application of optimization

The application of optimization in today’s world is really broad and there is almost no area of ​​industry that does not strive to optimize certain business processes. Whether it’s about the financial sector, production, distribution, energy, telecommunications, service activities, all the way to the public sector, and most often it’s about minimizing costs (production, transport, etc.) while maximizing profits. Thus, for example, the manufacturer wants to determine how to use limited amounts of raw materials to achieve the highest profit, and the manager how to distribute the given work among his employees so that the work is done in the shortest possible time.

Warehouse layout optimization

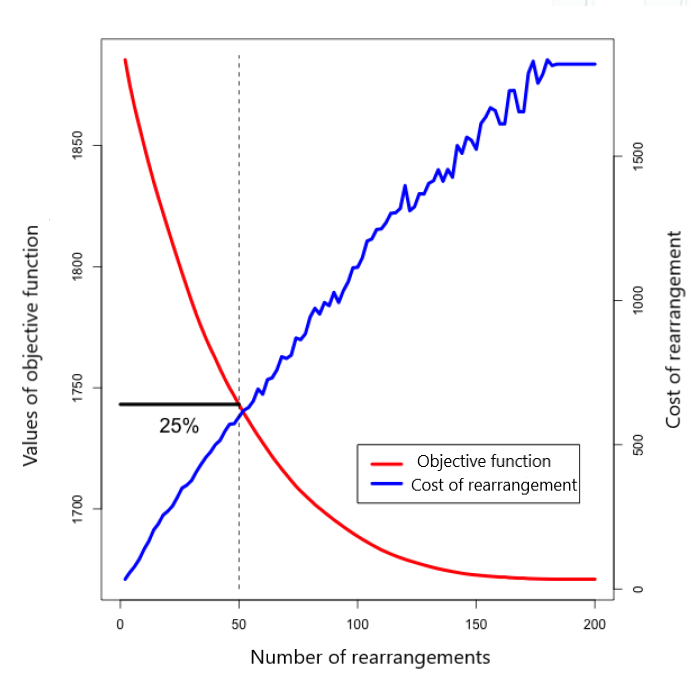
In all industries where there are warehouses, optimization is a key tool for minimizing inventory and warehouse personnel costs. In Megatrend poslovna rješenja, we have developed a solution for warehouse layout optimization. The optimization is carried out during the initial filling of the new warehouse (based on data on previous deliveries in the existing warehouse) but also during the relocation of already arranged goods in other warehouses (here, the consumption of picking time is minimized while limiting the consumption of the time required to move the items). After the mentioned initial filling, the optimization is started manually as needed and would suggest the grouping of low turnover items and moving them to the appropriate position in the warehouse.

The need to rearrange already arranged goods arose due to changes in product output caused by changes in popularity (trends) and changes in output caused by seasonality. One limitation for this model was that the rearrangement price must not be higher than some predetermined price, and the second was that the number of rearranged products must not be higher than allowed. Additionally, a module was included that was activated during the introduction of some new products, and during its execution, the warehouse was rearranged while respecting the maximum allowed number of items moved.

The process in the warehouse proceeded as follows: WMS (Warehouse Management System) creates picking lists, i.e. tables with supplier code data, a list of products and their quantity. Then, based on each such list, the order in which the forklift collects the products is calculated. The assumption was that this order is calculated by solving the optimization problem from the traveling salesman class (one of the most famous optimization problems). The function to be minimized in this problem is the total distance traveled between the products in the list. Since the value of this function depends on the distance between individual selected products, our goal was to enable the finding of a shorter optimal route later by better arranging the product obtained by optimization.

Problem setting

The key thing when solving an optimization problem is a precise mathematical formulation and a good setting of goals and constraints. So the mathematically formulated task was to distribute N products to M positions in the warehouse defined by the floor plan.

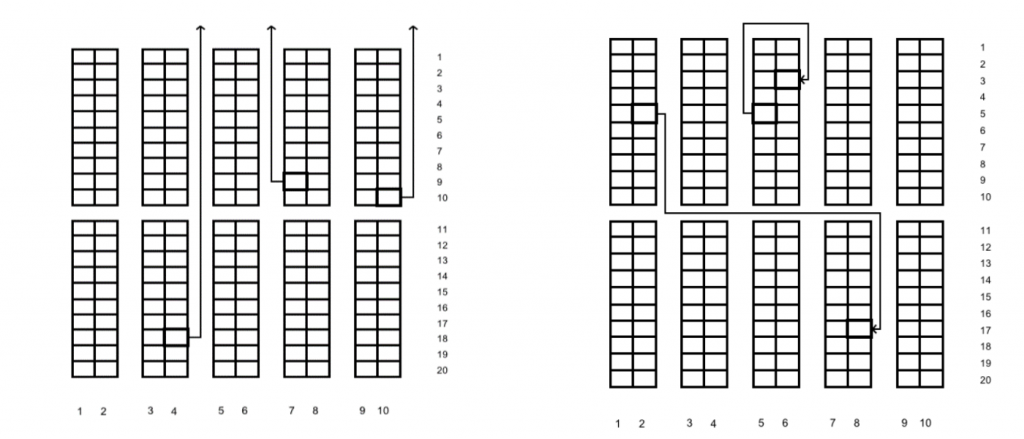
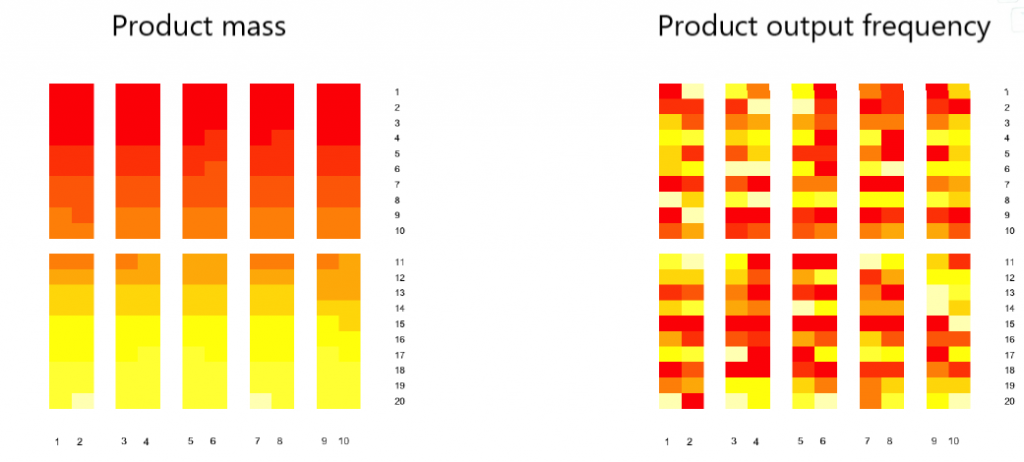
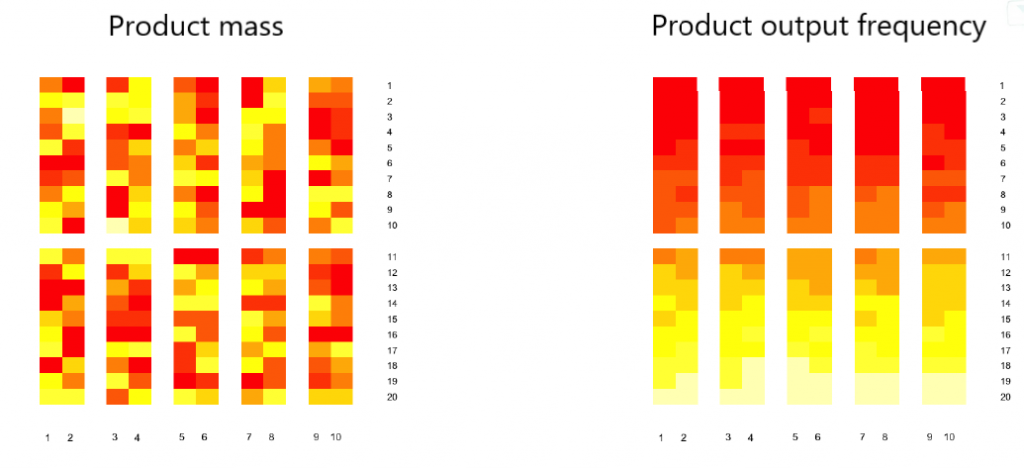
To do this, we needed to define the criteria by which we would decide if the product should be moved and if so, where. The first criterion was based on the output of an individual product (i.e. the frequency of appearance of that product on the picking lists) and was reduced to minimizing the distance of high-frequency products from the exit from the warehouse. The second criterion was of a more technical nature and was based on the minimization of the distance of products of large mass from the exit. The influence of these two criteria was regulated by entering appropriate weighting factors in the objective function that we optimized. For example, if we set the weight to mass equal to zero, we observe an optimization without the effect of mass on the picking order.

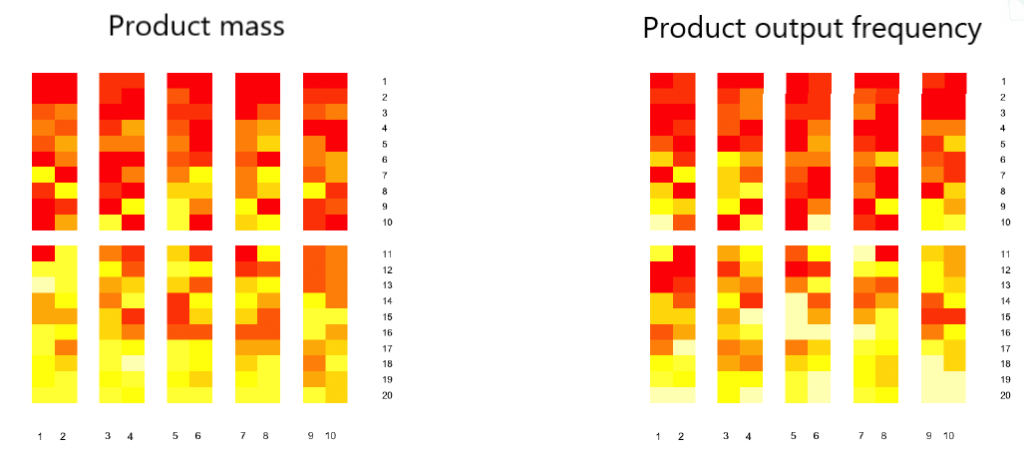
In an optimization problem, there are some constraints on the objective function that needs to be minimized (maximized). In our case, it was about the following restrictions: each product had to be placed in exactly one position, as well as that it was possible to place at most one product in each position, and that in each zone there are products of the same type. Namely, the warehouse was divided into zones where similar groups of items were located and it was assumed that products of different types should not be located in the same zone.

Solution to the problem

Our objective function represented the weighted sum of product-to-output distances with respect to outputs and the weighted sum of product distances with respect to mass. Weights in the sum were influenced by several factors. Each of the suppliers was assigned its importance (which was determined based on profit or some other criterion). Then, each product was associated with its frequency, and for each product its expected quantity was calculated in one picking list. We formulated the solution to the problem of optimal product arrangement with a matrix that told us that a certain product is located in a certain position.